Re-orthogonalization of PLS Algorithms
Aug 23, 2010
Thanks to everybody that responded to the last post on Accuracy of PLS Algorithms. As I expected, it sparked some nice discussion on the chemometrics listserv (ICS-L)!
As part of this discussion, I got a nice note from Klaas Faber reminding me of the short communication he wrote with Joan Ferré, “On the numerical stability of two widely used PLS algorithms.” [1] The article compares the accuracy of PLS via NIPALS and SIMPLS as measured by the degree to which the scores vectors are orthogonal. It finds that SIMPLS is not as accurate as NIPALS, and suggests adding a re-orthogonalization step to the algorithms.
I added re-orthogonalization to the code for SIMPLS, DSPLS, and Bidiag2 and ran the tests again. The results are shown below. Adding this to Bidiag2 produces the most dramatic effect (compare to figure in previous post), and improvement is seen with SIMPLS as well. Now all of the algorithms stay within ~1 part in 1012 of each other through all 20 LVs of the example problem. Reconstruction of X from the scores and loadings (or weights, as the case may be!) was improved as well. NIPALS, SIMPLS and DSPLS all reconstruct X to within 3e-16, while Biadiag2 comes in at 6e-13.
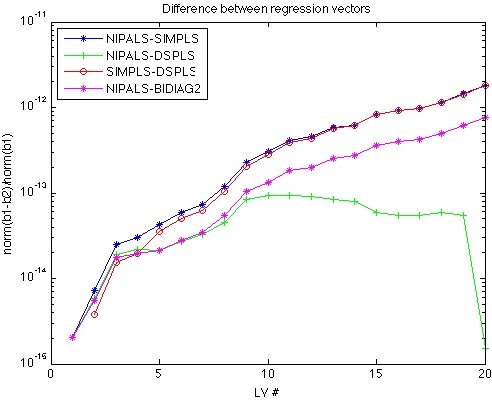
The simple fix of re-orthogonalization makes Bidiag2 behave acceptably. I certainly would not use this algorithm without it! Whether to add it to SIMPLS is a little more debatable. We ran some tests on typical regression problems and found that the difference on predictions with and without it was typically around 1 part in 108 for models with the correct number of LVs. In other words, if you round your predictions to 7 significant digits or less, you’d never see the difference!
That said, we ran a few tests to determine the effect on computation time of adding the re-orthogonalization step to SIMPLS. For the most part, the effect was negligible, less than 5% additional computation time for the vast majority of problem sizes and at worst a ~20% increase. Based on this, we plan to include re-orthogonalization in our SIMPLS code in the next major release of PLS_Toolbox and Solo, Version 6.0, which will be out this fall. We’ll put it in the option to turn it off, if desired.
BMW
[1] N.M. Faber and J. Ferré, “On the numerical stability of two widely used PLS algorithms,” J. Chemometrics, 22, pps 101-105, 2008.

 SEARCH
SEARCH